반응형
문제:
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
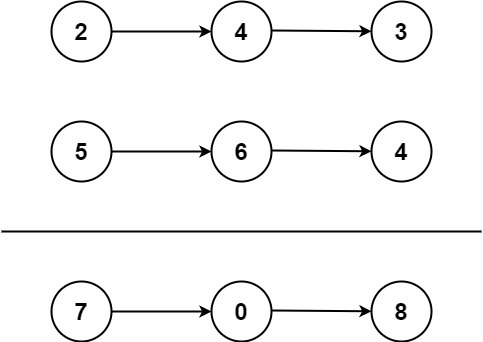
두 개의 링크 리스트를 받아와 각 리스트를 역순으로 뒤집어 합을 구한 뒤 다시 링크 리스트로 반환해주는 문제입니다.
알고리즘을 풀면서 문제를 단위별로 쪼개는 연습을 하고 있습니다.
class Solution:
#두개 숫자를 합해주는 함수
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
#링크리스트를 리스트로 변환해주는 함수
def toList(self, node: ListNode) ->List:
#링크리스트를 뒤집어주는 함수
def reverseList(self, head: ListNode)-> ListNode:
#리스트를 링크리스트로 변환해주는 함수
def toReverseLinkedList(self, result: str) -> ListNode:문제를 보자면 링크 리스트를 뒤집어주는 함수가 필요하고, 뒤집어진 링크 리스트를 리스트로 바꿔 연산을 한 뒤, 링크 리스트로 바꾸어 반환해주는 순서가 필요합니다. 이렇게 초반에 어떠한 기능이 필요한지 틀을 잡고 작성해가야 합니다.
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
l1_list = self.toList(self.reverseList(l1))
l2_list = self.toList(self.reverseList(l2))
resultStr = int(''.join(str(s) for s in l1_list)) + int(''.join(str(s) for s in l2_list));
return self.toReverseLinkedList(str(resultStr));
#링크리스트를 리스트로 변환해주는 함수
def toList(self, node: ListNode) ->List:
list: List =[]
while node:
list.append(node.val)
node = node.next
return list
#링크리스트를 뒤집어주는 함수
def reverseList(self, head: ListNode)-> ListNode:
node, prev = head, None
while node:
next, node.next = node.next, prev
prev, node = node, next
return prev
#리스트를 링크리스트로 변환해주는 함수
def toReverseLinkedList(self, result: str) -> ListNode:
prev: ListNode = None
for i in result:
node = ListNode(i)
node.next = prev
prev = node
return node이렇게 기능별로 나누어 풀면 중복 사용하는 코드들을 줄여주고, 로직의 흐름을 잘 파악할 수 있는 장점이 있습니다.
반응형
'혼자 공부하는 것들 > 알고리즘' 카테고리의 다른 글
| 94. Binary Tree Inorder Traversal (leetcode Python) +DFS로 풀기 (0) | 2021.11.02 |
|---|---|
| 200. Number of Islands (leetcode python) +DFS로 풀기 (0) | 2021.10.29 |
| [JS] 프로그래머스 약수의 개수와 덧셈 (0) | 2021.10.21 |
| 유클리드 호제법 (최대공약수, +최소공배수) (0) | 2021.10.03 |
| 에라토스테네스의 체 (0) | 2021.09.02 |

댓글